Dimensionality reduction is the process of reducing the number of random variables under consideration by obtaining a set of principal variables. It can be divided into feature selection and feature extraction.
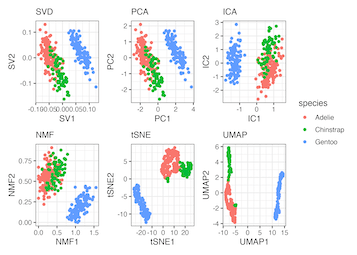
- Principal Component Analysis (PCA): Reduces the dimensionality of the data by selecting the most important features that capture maximum information.
- Principal Component Regression (PCR): PCR is a regression technique that is based on PCA. It’s used for building predictive models with high-dimensional data.
- Partial Least Squares Regression (PLSR): PLSR is a technique that combines features to reduce dimensionality.
- Sammon Mapping: Reduces dimensionality while preserving the structure of inter-point distances in high-dimensional space.
- Multidimensional Scaling (MDS): Aims to place objects in N-dimensional space so that their distances are preserved.
- Projection Pursuit: Finds the most interesting projection for high-dimensional data.
- Linear Discriminant Analysis (LDA): Used to find a linear combination of features that characterizes or separates two or more classes of objects or events.
- Mixture Discriminant Analysis (MDA): A generalization of LDA that involves a mixture of Gaussians.
- Quadratic Discriminant Analysis (QDA): A variant of LDA where each class uses its own estimate of variance.
- Flexible Discriminant Analysis (FDA): Combines features in a non-linear way to maximize class separability.
- Regularized Discriminant Analysis (RDA): Combines LDA and QDA.
- Partial Least Squares Discriminant Analysis: A variant of PLSR used in classification.





2 responses to “Dimensionality Reduction Algorithms”
Wonderful article! This is the type of information that are supposed to be shared around the net.
Disgrace on the seek engines for not positioning this post upper!
Come on over and seek advice from my website . Thanks =)
This piece was both informative and engaging. I particularly enjoyed the way the author broke down the subject matter. It sparked a lot of ideas for me. What do you all think about this?